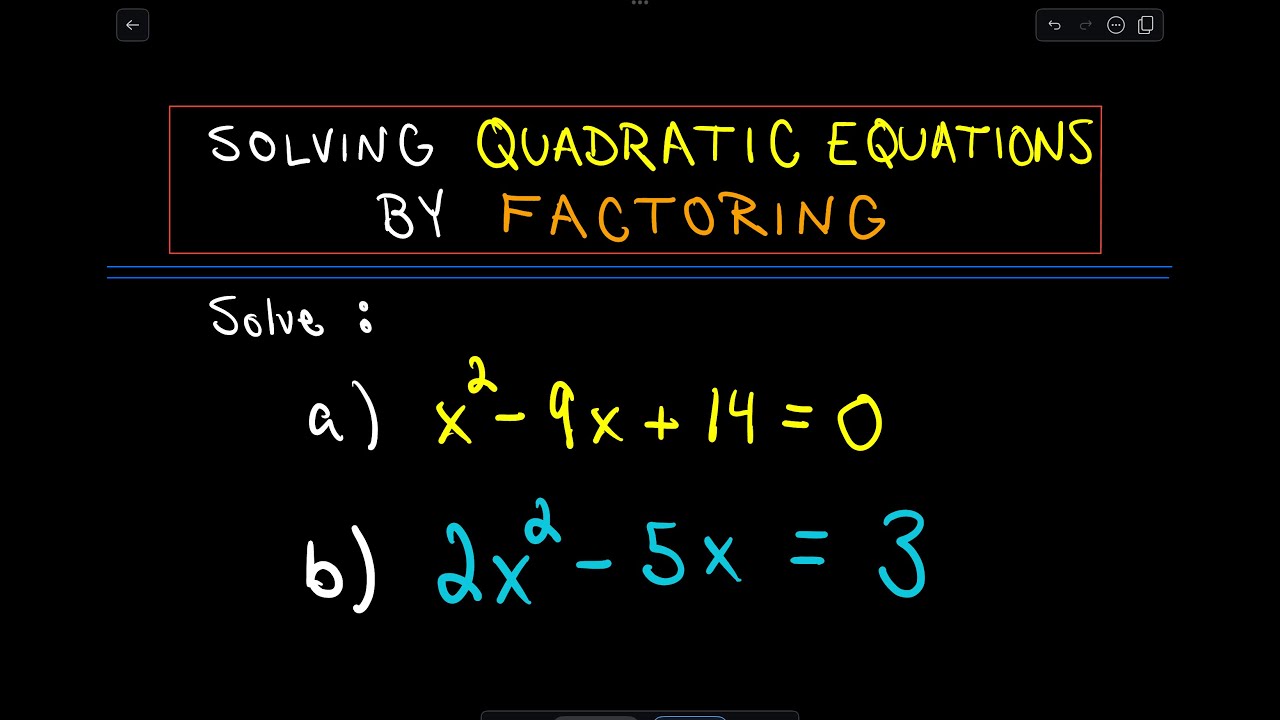Déchiffrer l'équation x²-9=0 : Le secret des solutions
Imaginez pouvoir déverrouiller les secrets d'une équation mathématique d'apparence complexe. L'équation x²-9=0, aussi simple qu'elle puisse paraître, ouvre la porte à un monde de possibilités en algèbre. Comment la résoudre par factorisation ? Découvrons ensemble cette technique élégante et efficace.
Résoudre x²-9=0 par factorisation, c'est un peu comme trouver la clé d'un coffre au trésor. Cette méthode, loin d'être une simple formule magique, repose sur la reconnaissance d'identités remarquables. En comprenant la structure de l'équation, on peut la décomposer en éléments plus simples et ainsi révéler ses solutions.
L'importance de la factorisation dans la résolution de x²-9=0 réside dans sa simplicité et son élégance. Elle permet de contourner les calculs complexes et offre une approche intuitive pour trouver les valeurs de x qui satisfont l'équation. Mais attention, des pièges peuvent se cacher. Il est crucial de bien maîtriser les identités remarquables pour éviter les erreurs.
L'équation x²-9=0 est une équation du second degré, ce qui signifie que la variable x est élevée à la puissance 2. La résolution par factorisation exploite l'identité remarquable a²-b² = (a+b)(a-b). En reconnaissant que 9 est le carré de 3, on peut réécrire l'équation sous la forme x²-3²=0.
En appliquant l'identité remarquable, on obtient (x+3)(x-3)=0. Ce qui signifie que soit (x+3)=0, soit (x-3)=0. On en déduit alors les deux solutions : x=-3 et x=3. Voilà, le mystère de x²-9=0 est résolu grâce à la factorisation.
La factorisation de x²-9=0 trouve ses racines dans l'histoire de l'algèbre. Depuis des siècles, les mathématiciens ont cherché des méthodes pour résoudre les équations. La factorisation est apparue comme une technique puissante et polyvalente, applicable à de nombreuses situations.
Exemple : Imaginez un carré de côté x. Si on enlève un carré de côté 3, la surface restante est nulle. Cela se traduit par l'équation x²-9=0. Les solutions x=3 et x=-3 représentent les côtés du carré initial.
Avantages de la factorisation : simplicité, rapidité, et compréhension approfondie des équations.
Plan d'action : 1. Identifier l'identité remarquable. 2. Factoriser l'équation. 3. Trouver les solutions.
FAQ :
1. Qu'est-ce que la factorisation ? Décomposer une expression en un produit de facteurs.
2. Pourquoi utiliser la factorisation pour résoudre x²-9=0 ? C'est une méthode simple et efficace.
3. Quelles sont les solutions de x²-9=0 ? x=3 et x=-3.
4. Qu'est-ce qu'une identité remarquable ? Une égalité toujours vraie.
5. Comment vérifier les solutions ? En les remplaçant dans l'équation initiale.
6. Peut-on utiliser d'autres méthodes pour résoudre x²-9=0 ? Oui, comme la méthode du discriminant.
7. Est-ce que la factorisation fonctionne pour toutes les équations du second degré ? Non, seulement pour certaines.
8. Où puis-je trouver plus d'informations sur la factorisation ? Dans les manuels scolaires et sur internet.
Conseils et astuces : Pratiquez régulièrement la factorisation pour la maîtriser. Identifiez les identités remarquables dès le début.
En conclusion, résoudre x²-9=0 par factorisation est une technique essentielle en algèbre. Elle permet de décomposer l'équation en éléments simples et de trouver les solutions rapidement. En maîtrisant cette méthode, vous ouvrez la porte à la résolution d'équations plus complexes et approfondissez votre compréhension des mathématiques. N'hésitez pas à pratiquer et à explorer d'autres identités remarquables pour devenir un as de la factorisation !
Defi du code niveau 47 partie 1 laventure continue
Lodyssee de cour en cour un voyage au coeur de la complexite
La magie dune veilleuse reine des neiges
